Classroom Connections July 19, 2025

Content ideas and data for math and statistics classes

Classroom connections are less about immediate application and more about me pointing out resources. I believe that there is a lot of amazing math, statistics, and data out there that might be used in math classrooms and is also intriguing to the curious. Simultaneously, when someone inquires about the applications of math, consider these numerous examples.

Some of these examples may require some effort to be classroom-ready, and some of the material has appeared in previous QTRS posts. I’m ordering the content roughly based on the level of math. Please tell me if you or someone you know uses any of these suggestions in the classroom or has a relevant idea (email me at thomas.pfaff@sustainabilitymath.org). I encourage you to leave a comment, as your feedback motivates me to continue this work, or send me an email if you find these classroom connection posts useful. Similarly, if you have an opinion or concept that is relevant, please share it in the comments. Please share, like, subscribe, and comment.

Interactive graphic and data

The National Snow and Ice Data Center Chartic Interactive Sea Ice Graph has multiple uses in quantitative literacy or data-based courses. In a calculus class, you can also discuss concepts such as max, min, and inflection points (units and interpretation are particularly intriguing). On the right sidebar, you can choose which years to display. The menu (three bars) allows you to download the data and graphs.

Interpreting graphs and more

Predictive musculoskeletal simulations reveal the mechanistic link between speed, posture and energetics among extant mammals (10/4/2024) from the journal Nature Communications. The graph here is one of many (note the log scale) that can be used in a stats or any quantitative or data course. All data is available, as well as the R code to create the figures.

A range of modeling

Unraveling the Impacts: How Extreme Weather Events Disrupt Wood Product Markets (9/5/2024) from the journal Earth’s Future.

A nice use of a logistic model, which could be used in numerous classes as the function V(A).

Additionally, the paper includes a more complex example that utilizes integrals and summations. At the very least, this paper provides an example of how calculus is applied.

Maps, graphs, and modeling

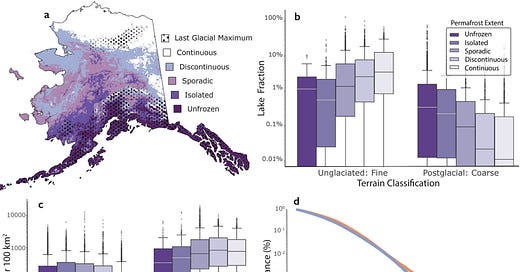
Glacial History Modifies Permafrost Controls on the Distribution of Lakes and Ponds (2/14/2025) from the journal Geophysical Research Letters. Students in stats and other courses that emphasize interpreting graphical information can utilize the graph below. Data for the paper is available at a link at the bottom.

Plain language summary:

Lakes and ponds are key indicators of the Arctic's vulnerability to rapid warming. Their presence influences the water cycle, wildlife habitat, permafrost temperatures, and the balance between carbon storage and release to the atmosphere. Scientists expect permafrost thaw to cause lake area to decline over time, representing a major shift in the landscape with consequences for ecosystems, water resources, and carbon cycling. The extent of lake drainage across the northern permafrost zone remains unclear, especially given recent studies that have found both increasing and decreasing lake area. Here, we demonstrate that differences in glacial history and geology can explain many of the conflicting trends reported in these previous studies. We show that thawing permafrost tends to reduce lake area in regions without past glaciation. However, in regions shaped by glaciers, lake areas can slightly increase with permafrost thaw. To do this, we use the new the Alaska Lake and Pond Occurrence Data set, which maps over 800,000 lakes and ponds and their seasonal fluctuations in unprecedented detail. We discuss potential mechanisms for long-term landscape evolution to influence modern lake responses to permafrost thaw. Finally, we use our results to improve projections of future changes to lake area across Alaska.

Game Theory

A complete classification of evolutionary games with environmental feedback (10/10/2024) in PNAS Nexus. Certainly good for an independent study, and maybe the graphs are useful in some classes. The abstract:

A tragedy of the commons, in which rational behavior of individuals to maximize their own payoffs depletes common resources, is one of the most important research topics in game theory. To better understand the social dilemma problem, recent studies have developed a theoretical framework of feedback-evolving game where individual behavior affects an environmental (renewable) resource and the environmental resource changes individual payoffs. While previous studies assumed that the frequency of defectors increases (prisoner's dilemma [PD] game) when the environmental resource is abundant to investigate an oscillating tragedy of the commons, it is also possible for other types of game to produce the social dilemma. In this paper, we extend the feedback-evolving game by considering not only PD game, but also the other three game structures when the environmental resource is replete for a reasonably complete classification. The three games are Chicken game where defectors and cooperators coexist through minority advantage, Stag-Hunt (SH) game with minority disadvantage, and Trivial game where the frequency of cooperators increases. In addition, we utilize a dilemma phase plane to visually track (transient) dynamics of game structure changes. We found that an emergent initial condition dependence (i.e. bistability) is pervasive in the feedback-evolving game when the three games are involved. We also showed that persistent oscillation dynamics arise even with Chicken or SH games in replete environments. Our generalized analysis will be an important step to further extend the theoretical framework of feedback-evolving game to various game situations with environmental feedback.

Please share and like

Sharing and liking posts attracts new readers and boosts algorithm performance. I appreciate everything you do to support Briefed by Data.

Comments

Please tell me if you believe I expressed something incorrectly or misinterpreted the data. I'd rather know the truth and understand the world than be correct. I welcome comments and disagreement. I encourage you to share article ideas, feedback, or any other thoughts at briefedbydata@substack.com.

Bio

I am a tenured mathematics professor at Ithaca College (PhD in Math: Stochastic Processes, MS in Applied Statistics, MS in Math, BS in Math, BS in Exercise Science), and I consider myself an accidental academic (opinions are my own). I'm a gardener, drummer, rower, runner, inline skater, 46er, and R user. I’ve written the textbooks “R for College Mathematics and Statistics” and “Applied Calculus with R.” I welcome any collaborations, and I’m open to job offers.